6-2. 모어원 그리는 방법 - 경사각 없을 때 (1)
앞의 6-1 포스팅에서 모어원을 그리기 위한 기본적인 배경지식을 알아봤습니다. 혹시 안읽어보셨다면 꼭 읽고 오시는게 좋습니다
어떻게 작도하는지 막연하게 설명해드려도 좋으나, 예제를 몇 개 가지고 구체적인 숫자로 설명해드리는게 더 쉬울 것 같습니다.
■ 평면응력만 주어졌을 때 최대/최소 주응력 구하는 문제 (경사각 X)
원래 모어원의 궁극적인 목적은 어떤 요소의 '특정 각도 θ에서 회전한 경사면에서의' 응력요소를 구하는 것이지만, 경사각 없이 수직, 전단응력만 준 다음에 최대/최소 주응력을 구하라고 하는 문제가 있습니다.
이 또한 복잡하고 긴 공식으로 풀 수 있지만, 피타고라스만 안다면 공식 없이 풀 수 있습니다.

자 문제의 응력조건을 그림으로 한번 정리해봅시다.
반대로 아래 그림만 주어졌을 때도 위 처럼 응력조건을 쓸 수 있어야 합니다. 제대로 쓰려면 특히 '전단부호의 뱡향' 을 헷갈리지 않아야겠죠.
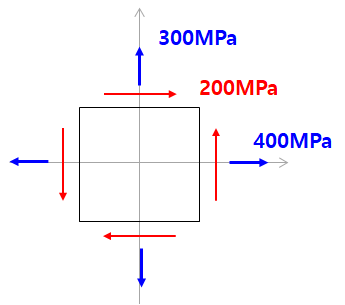
이제 모어원을 작도해보겠습니다.
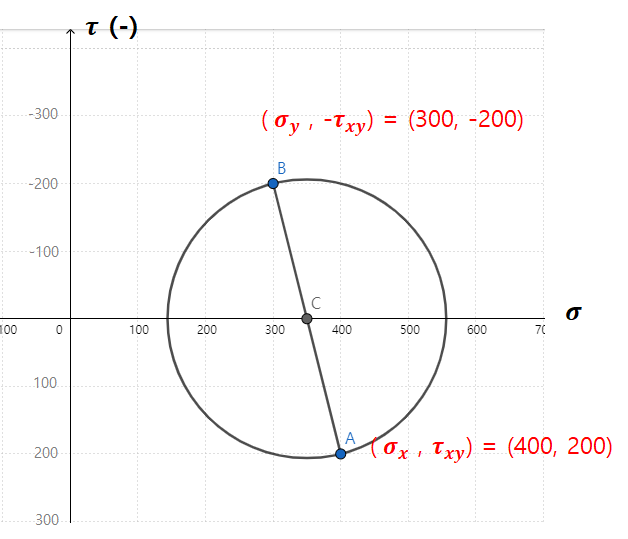
1. 모어원의 좌표계에 두 개의 점 A (σx, τ) , B (σy, -τ) 를 찍습니다.
- 항상 첫번째 점 A 에서 전단응력 자리는 주어진 τ값 그대로 넣고, 점 B 전단응력 자리는 -τ값 넣기.
A, B점의 세로축 요소는 부호만 다르고 항상 대칭입니다.
애초에 전단응력 값이 - 였다면, A점은 가로축 기준으로 위쪽에, B점은 아래쪽에 찍힐 것입니다.

2. A, B 두 점을 잇는 선을 그리고, 그 선분을 지름으로 하는 원을 그립니다. (모어원)
-
여기에서 두 점을 알고 있으니, 당연히 원의 중심 (선분의 중점) 을 구할 수 있습니다.
굳이 식으로 표현하자면 (σx + σy) / 2 겠죠?
3. A, B 직선을 빗변으로 하는 직각삼각형을 그립니다. 피타고라스로 빗변의 길이를 구하고, 빗변길이는 곧 원의 지름입니다.
- 우리는 A, B 의 좌표를 알고있으므로 직각삼각형의 가로, 세로 길이를 이미 알고 있습니다. 피타고라스를 이용해서 빗변의 길이를 구하면 그게 바로 원의 지름이 되며, 계산하면 412 가 나옵니다.
- 그리고 y축 전단응력 값은 하나만 주어지고 A, B점 값은 서로 부호만 다르다고 했습니다. 즉 삼각형의 높이는 항상 [전단응력 절대값 x 2] 가 되겠죠.

4. 최대, 최소 주응력은 가로축 (σ축) 을 지나는 모어원 위에 있다고 6-1에서 공부했습니다.
즉 원의 중점에서 원의 반지름만큼 더하고 뺀 값이 최대, 최소 주응력입니다.

5. 문제에서는 안물어봤지만, '재료내에 발생하는 최대 전단응력값' 도 구할 수 있습니다.
-
6-1포스팅 가장 마지막에 다뤘듯이, 최대 전단응력값 = 원의 반지름값, 206 입니다.

쓰다보니 길어져서, 일단 한 문제만 보고 마무리하겠습니다.
요소를 경사면 관점에서 보진 않았지만, 모어원 좌표계에서 어떻게 원을 그리는지 알아보았습니다. 이것만 알면 각도 적용해서 경사면 응력요소 구하는것도 금방 할 수 있습니다. (저 위에서 한 과정만 더 하면 됩니다)
설명하느라고 풀어써서 풀이가 긴 것 같은데, 푸는법만 알면 좌표에 원 하나랑 삼각형만 그리면 끝납니다.
다음포스트에는 경사각이 있는 문제로 돌아오겠습니다.
모어원개념,모어원설명,모어원작도,모어원문제,모어원공식,모어원이란,모어원부호,모어원그리는방법,최대주응력,모어서클그리기