■ 차원해석 (Dimensional Analysis)
차원해석은 각종 물리량의 단위 차원을 가지고, 각 물리량과의 관계를 해석하는 방법입니다.
기본차원은 아래와 같습니다.
- MLT차원계 : 질량[M], 길이[L], 시간[T]
- FLT차원계 : 힘[F], 길이[L], 시간[T]
ex) 속도는 m/s → [LT-1]
ex) 힘 F=ma에서 kg m/s^2 → [MLT-2]
* 버킹엄의 파이 정리 : 차원해석 방법의 하나로, 무차원 변수를 얻는 방법입니다.
어떤 물리현상의 관련변수가 k개, 그리고 k라는 변수들을 이루는 (=변수를 표현하는) 최소한의 기준차원(기본차원) 개수가 r개라고 하면, 관련된 무차원수는 k-r개 유도할 수 있습니다.
보통 기사책에는 π (독립무차원수) = n - m 으로 표현되어있는데 k - r과 같다고 보시면 됩니다. 즉,
π (독립무차원수) = n-m = k-r
(n,k : 물리량(변수)의 수 / m,r : 앞의 물리량을 이루는 기본차원의 수)
■ 상사법칙 (Similarity law) 이란?
Similarity, 말그대로 '닮은, 비슷한' 법칙 이라는 뜻입니다.
어떠한 현상의 실험을 하고싶은데 자연현상을 우리가 임의로 실험한다거나, 거대한 실제 구조를 만들기엔 어렵습니다.
그래서 우리는 주로 실험을 할 때 축소 모형을 만들거나 비슷한 실험조건을 갖춰서 실험을 하게 됩니다. 이렇게 축소모형의 실험 결과를 실제 원형조건으로 환산하는 것을 말합니다.
우리가 뭔가 물리량을 비교할 때는 보통 비율로 비교를 합니다. 즉 어떤 특정 변수를 조정하면, 실제로 어떤 특성이 몇 배가 증감하는지를 알려면 '무차원'이어야 합니다. 흔히 생각하는 2배, 3배는 단위가 없는 숫자(비율) 이니까요.
이러한 무차원 상사법칙을 도출하기 위해서 위와 같은 '차원해석'이 이뤄집니다.
그럼 시험에 자주나오는 상사법칙(무차원수) 에 대해 아래와 같이 정리해보겠습니다.
사실 다 이해가 되지는 않는데요,, 개념만 알고있으면 문제를 보자마자 바로 맞출 수 있는 보너스 분야이기도 합니다.
특히 레이놀즈수는 너무너무 중요해서, 나중에 또 따로 다루겠습니다.
참고로 상사법칙에서 중요한것은 정의도 중요하지만, 그 무차원수가 쓰이는 응용분야를 아는것도 중요합니다. 문제에서 자주 나오곤 하는 듯 합니다.
※ 표는 컴퓨터, 태블릿 화면에서 보시는게 가시성이 더 좋습니다.
| 구분 | 정의 | 보충 |
| 레이놀즈수 |  |
* 강제대류에서의 층류와 난류를 구분하는 척도 * 응용분야 : 양력, 항력, 관로 내 마찰손실(관유동), 경계층유동, 잠수함(=어뢰), 파이프 등 |
| 프루드수 | 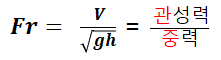 |
* 응용분야 : 자유표면을 갖는 유동, 개수로, 선박(배), 파고저항, 강에서의 모형실험, 조파현상, 수차, 수력도약 * 왼쪽의 분모 h는 수심(or직경) 을 의미합니다. 경우에 따라 ℓ 혹은 L로 표현하기도 합니다. |
| 코시수 |  |
* 압축성 유체의 운동 |
| 웨버수 |
* 응용분야 : 기체-액체 or 액체-액체상의 경계면, 표면장력파, 오리피스, 위어, 물방울 형성, 작은 직경의 관 내에서의 유동 * 표면(계면)장력의 영향을 나타내며, We가 작을수록 표면장력이 크다는 의미입니다. |
|
|
오일러수 |
 |
* 유체의 유동은 유체 내 두 지점에서의 정압차이(압력차)에 의해 만들어집니다. 또한 관성력은 동압으로 볼 수 있습니다. * 즉 정압/동압 으로도 표현 가능합니다. 잘 안외워지면 압 = (구)정동 으로 외우기 |
| 마하수 | 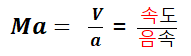 |
* 응용분야 : 압축성유동 (풍동실험, 고속 항공기, 로켓 등) * Ma<0.8인 경우 아음속 (책에는 1로 나와있는 경우도 있습니다), 보통 이 영역에선 유체를 비압축성이라고 가정할 수 있음 * Ma<0.3인 경우 기체 또한 비압축성으로 가정할 수 있음
* 음속 a에 대한 참고식 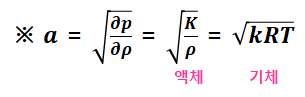 |
| 프란틀수 |  |
* 동점성에 대한 열분자 확산도의 비. 강제대류의 열전달 특성 * 기체에서의 프란틀수는 0.7 , 엔진오일은 약 100~4만 → Pr 크면 확산정도가 열<운동으로, 열확산이 느림 → Pr 작으면 확산정도가 열>운동으로, 열확산 잘됨 |
|
넛셀수 |
||
|
스트라홀수 |
 |
* Sr = fℓ / V로 표현하기도 하며, f는 진동수, ℓ 은 특성거리 (두께or직경 등) |
| 그라쇼프수 |  |
* 자연대류에서의 층류와 난류를 구분하는 척도 * 온도차에 의한 부력이 속도 및 온도분포에 미치는 영향 |
| 스테판수 |  |
|
| 푸리에수 |  |
* 비정상 열전도 상태를 나타내는 무차원수 |
| 레일리수 |  |
* (자연대류) 유체층 속에서 열대류가 일어나는지 여부를 결정 * 보통 대류 발생에 필요한 임계 레일리값을 1,000으로 봅니다. (Ra>1000 : 대류발생 / 그 이하는 '전도'형태로 열전달 |
추가해야할 내용이 있으면 지속적으로 업데이트 하겠습니다.
#상사법칙,무차원수,프루드수,코시수,웨버수,마하수,오일러수,프란틀수,넛셀수,누셀수,너셀수,스트라홀수,압력계수,그라쇼프수,스테판수,푸리에수,레일리수,강제대류,자유표면,어뢰,차원해석,버킹엄의파이정리,독립무차원수,
'STUDY > 기계공학-유체역학' 카테고리의 다른 글
| 참고2-2)유체역학-피토정압관 공식 유도 및정리 (11) | 2020.10.09 |
|---|---|
| 참고2-1)유체역학-유체계측 정리 (유체측정) (0) | 2020.10.09 |
| 1. 유체의 정의와 분류, 뉴턴의 점성법칙 (5) | 2020.05.01 |


