수직응력, 전단응력, 그리고 각도가 모두 주어진 예제 하나를 같이 보면서 경사각이 주어졌을 때의 모어원 문제는 어떻게 풀면 되는지 알아보겠습니다.
※ 풀이가 긴데요.. 설명하려니 풀어써서 그렇고, 방법만 숙지하시면 원 하나에 삼각형 몇개만 그리면 끝납니다.
|
■ 문제1  |
■ 풀이
본격적으로 풀기전에, 문제에서 주어진 조건을 정리해봅시다.
- σx = 10 MPa (화살표 방향이 인장)
- σy = -5 MPa (화살표 방향이 압축)
- τxy = -6 MPa (포스팅 6-1참조. 전단응력 부호는 화살표가 오른쪽 위를 향하면 +, 그 반대는 -)
- 경사각 : 45° (그림에서 원점기준 반시계방향으로 경사면이 형성되어있으므로, +로 생각)
자 그럼 이제 앞 포스팅 6-2에서와 같이, 차근차근히 모어원을 그려보겠습니다.
1. 모어원 좌표계에 두 개의 점 A (σx, τ) , B (σy, -τ) 를 찍습니다.
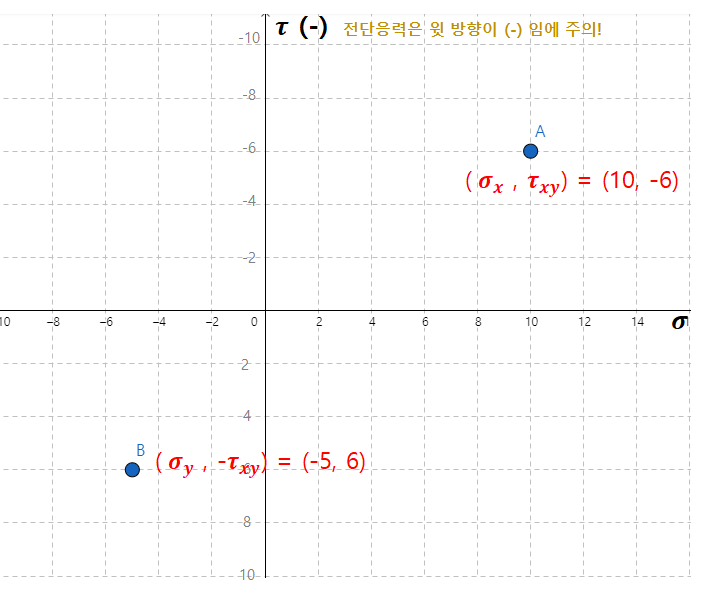
2. A, B 두 점을 잇는 선분을 그리고, 이를 지름으로 하는 모어원을 그립니다.
- 원의 중심점을 미리 파악해 놓습니다. ( 2.5 , 0 ) 이 됩니다.
- 앞에서도 말했지만 A, B 점의 전단응력 자리 값은 부호만 다르고 항상 대칭이므로, 원의 중심은 항상 가로축 (수직응력 축) 위에 놓여있게 됩니다.

3. 피타고라스로 원의 지름 (삼각형 빗변길이) 를 미리 파악해놓습니다.
- 직각삼각형의 가로, 세로를 알고있으니 빗변의 길이를 구할 수 있습니다. 19.2 입니다.
- 즉 원의 지름은 19.2, 반지름은 9.6이 됩니다.

3. 이제 경사각을 적용합니다. A-B 선분을 [경사각 x 2] 만큼 돌립니다.
- 경사각 부호가 +이면 반시계방향으로 돌리고, - 이면 시계방향으로 돌립니다.
- 여기서 중요한 것은 경사각을 적용해서 A-B선분을 모어원에서 돌릴 땐, 항상 경사각의 두 배 만큼 돌립니다. 즉 이 문제에서는 [45도 x 2] 인 90도만큼 돌리면 되겠습니다.
4. A-B선분을 회전시킨 자리에 새로운 선분 A'-B' 가 생겼습니다. 이제 이 선분에 우리가 구하고자 하는 특정 각 경사면에서의 응력 요소가 모두 있습니다.

|
※ 문제를 계속 풀기전에 각 응력값이 모어원 위에 어디에 있는건지 보고 가겠습니다. 1) 점 A, B를 이용해 원을 그린 후에는, 이 요소의 최대 최소주응력과 최대전단응력은 항상 아래와 같이 일정합니다. (각도를 얼마나 돌렸는지에 상관 없이) 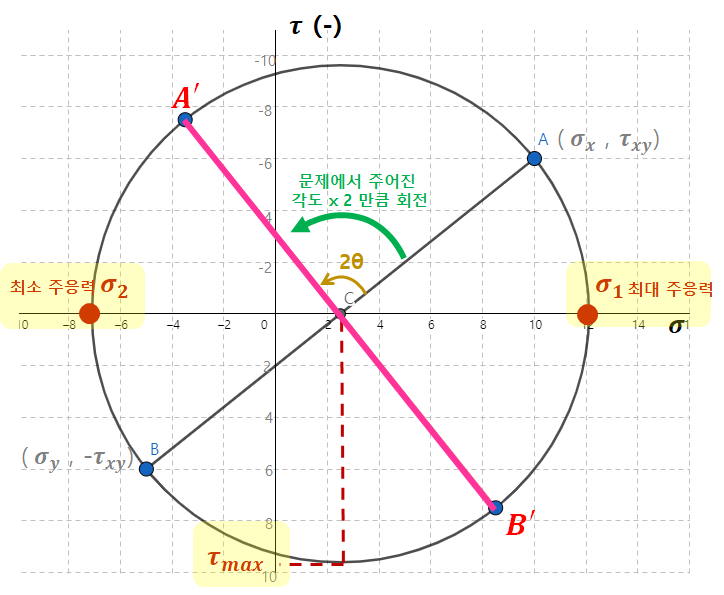
2) [θ만큼의 경사면에서 생기는 응력요소]들은 2θ만큼 회전한 A'-B'위에 있습니다.  |
5. 자, 그럼 우리가 구하고자 하는 응력요소 값은 A' 의 좌표값에 있습니다.
- A'의 x좌표가 문제에서 물어본 수직응력, y좌표가 전단응력이 됩니다.
- 직각삼각형을 이용해서 구합니다.
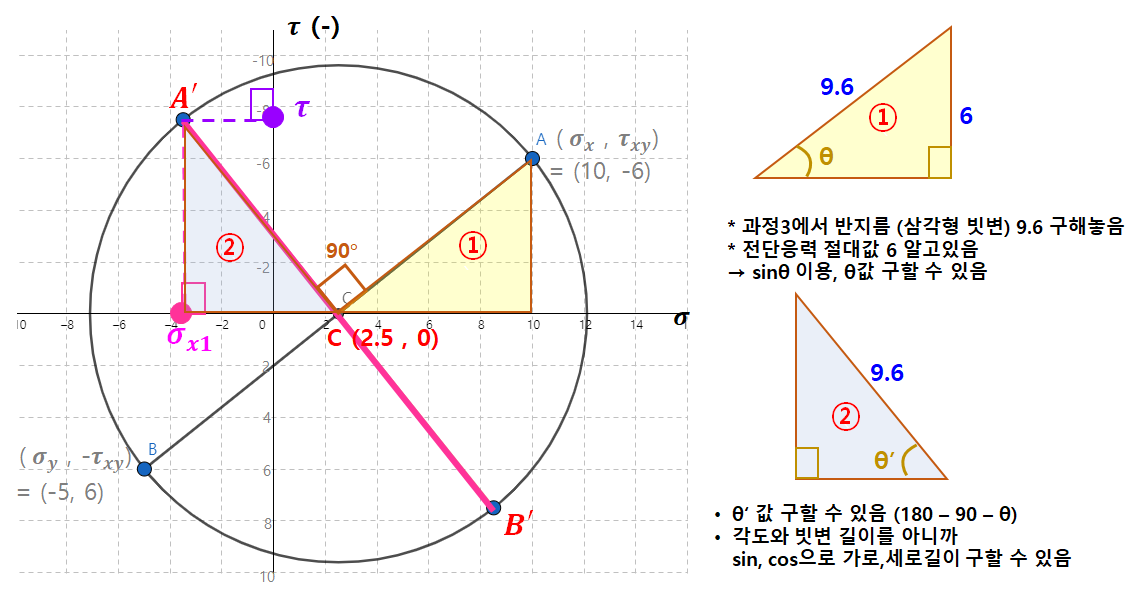
6. 이제 삼각형 길이들을 좌표 원점을 고려해서 좌표값으로 구해주면 됩니다.
- A'는 2사분면에 놓여있습니다. 모어원 좌표계에서 y축 윗방향이 (-)라고 하였으므로, 전단응력값이 - 입니다.
- 마찬가지로 수직응력 (σ x1) 도 2.5 - 6 = -3.5 가 나오게 됩니다.
- 답은 수직응력 = -3.5MPa, 전단응력 = -7.5MPa 입니다.
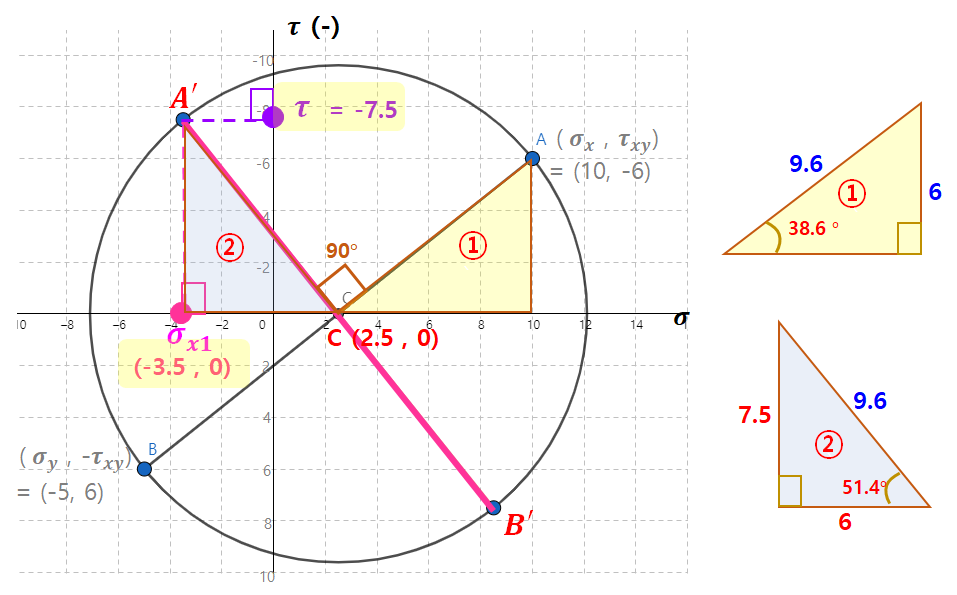
풀이가 길고 복잡한거같은데요... 자세히 차근차근 설명하려다 보니 길어진 것 뿐입니다 ㅠ_ㅠ 방법만 알면 쉬워요.
다음 포스팅에서는 예제 몇개 더 풀어보고 모어원 마무리 하겠습니다. 그 땐 풀이를 간단하게 포스팅하겠습니다.
# 모어서클그리기, #모어원그리기, #모어서클그리는법, #모어원그리는법, #모어원, #모어서클, #모어원수직응력,#모어원전단응력,모어원개념,모어원설명,모어원작도,모어원문제,모어원공식,모어원이란,모어원부호,
'STUDY > 기계공학 -재료역학' 카테고리의 다른 글
| 6-5. 모어원 문제풀이 (4) | 2019.11.15 |
|---|---|
| 6-4. 모어원으로 변형률 문제 풀기 (9) | 2019.10.31 |
| 6-2. 모어원 그리는 방법 - 경사각 없을 때 (1) (2) | 2019.10.26 |
| 6-1. 모어원 그리는 방법 - 배경지식편 (7) | 2019.10.26 |
| 5-3. 비틀림 탄성에너지, 코일스프링 (2) | 2019.10.22 |