※ 본 설명은 z축을 고려하지 않은 평면변형률 문제에 대한 설명입니다.
기사 시험공부를 하다보면 εx, εx, τxy, 최대 주변형률, 최대 전단변형률 등을 물어보는 문제가 있습니다.
뭔가 모어원 (σx, σy, τxy, 주응력, 최대전단응력 등) 과 형태가 비슷함을 알 수 있습니다.
이런 변형률 문제는 모어원을 똑같이 적용해서 풀 수 있습니다. 다만 우리가 약속했던 모어원 좌표계에서, 전단응력 축의 값이 다릅니다.
■ 평면응력과 평면변형률 비교 및 좌표계
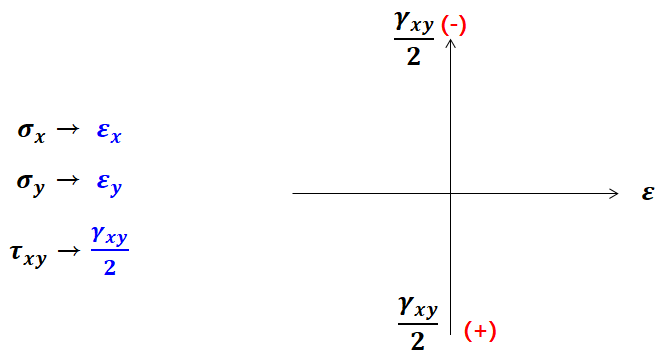
즉, y축인 전단응력축 τ 자리에 전단변형률/2 값이 들어간다는 사실만 알고 있으면 모어원과 똑같이 풀 수 있습니다.
앞에서 모어원에 대한 충분한 풀이는 (6-1 ~ 3) 다뤄봤으니, 간단하게 Goodno 책에 있는 예제 하나 풀어보겠습니다.
※ 모어원 그리는법 아래 글 참조 (6-1 ~ 3)
2019/10/26 - [STUDY/기계공학 -재료역학] - 6-1. 모어원 그리는 방법 - 배경지식편
6-1. 모어원 그리는 방법 - 배경지식편
Mohr's circle, 모어원(모어서클) 은 기사시험에도, 그리고 공기업 전공시험에도 단골로 나오는 문제입니다. 그런데 책을 피면 이보다 더 공식이 복잡하고 어려울 수 없습니다. 저는 개인적으로 저런 긴 공식들을..
alliebird.tistory.com
|
■ 문제1  (a) 각 θ = 30° 방향의 요소에 대한 변형률 |
■ (a) 풀이
위에 그림1에서 봤듯이 수직응력 자리에는 x,y 변형률, 그리고 전단응력 자리에는 전단변형률/2 가 들어갑니다. 바로 그림으로 보겠습니다.
문제 조건에 붙은 숫자 뒤 10^(-6)은 어차피 나중에 한꺼번에 붙여주면 되니까 제외하고, 앞의 숫자만 가지고
1. 두 점 A,B를 찍습니다.

2. A,B를 지름으로 하는 원을 그리고, 구할 수 있는 모든 값을 구해놓습니다.
문제 (a)에서 30도 경사에 대한 변형률을 구해야 하니, A-B선분을 30°x2배 회전해야 할 것입니다.
x축과 A-B 선분 사이의 각도를 알고 있어야 60도 회전했을 때 각 또한 알 수 있으므로, 이것도 구해놓습니다.
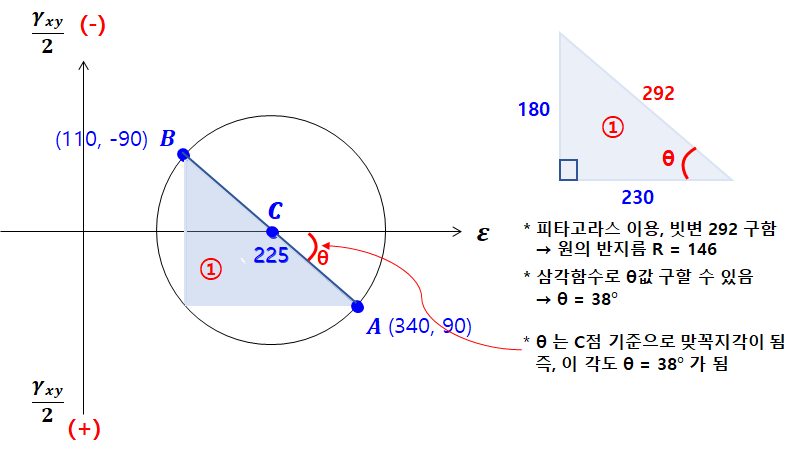
3. A-B 선분을 30° x 2 = 60도 회전합니다.
문제에서 (-) 부호가 따로 없으니, 양의방향이라고 생각하고, 반시계방향으로 돌립니다.
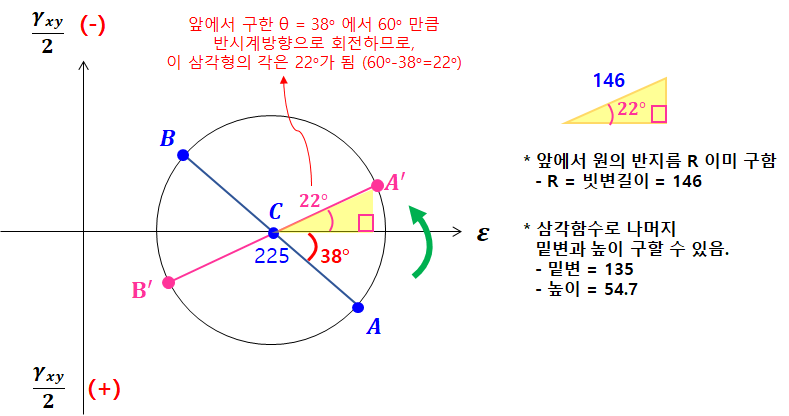
4. 이제 삼각형 길이를 A'와 B'의 좌표로 변환해줍니다.
여기서 30도 회전된 상태의 전단변형률을 구할 땐, 직각삼각형 높이 값이 τxy ÷ 2 되어있는 상태임을 기억합니다.
반드시 x 2를 해줘야 답이 됩니다.
회전된 요소의 전단응력/변형률은 모두 A' 의 좌표를 기준으로 생각하고, 부호도 그대로 따라가면 됩니다.

참고로 Goodno 책 답에는 전단변형률 값이 -110 x 10^(-6) 으로 되어있는데, 책에서는 긴 공식에 숫자만 대입해서 푼거라서 두 풀이차이에 의한 계산오차로 판단됩니다. 만약 객관식이었다면 가장 비슷한 값을 고르면 될 것 같습니다.
■ (b), (c) 풀이
위에서 구할건 다구했습니다. 모어원에서 각 좌표값이 의미하는 바는 6-3에서 다뤘습니다. (중간부분 참조)
R=146이고, 원 중심이 (225,0) 이니
- 최대주변형률 (ε1) = 225 + 146 = 371
- 최소주변형률 (ε2) = 225 - 146 = 79
- 최대전단변형률 ÷ 2 = R = 146 이므로, 곱하기 2 한 292가 답입니다.

역시나 책에서는 삼각형으로 안풀고 공식에 대입해서 답이 각각 370, 80, 290 으로 되어있는데 이 또한 계산오차로 생각하면 되겠습니다.
|
■문제2 주변형률이 a, 5a일 때 최대 전단변형률은? |
■풀이
문제 자체에서 주변형률 2개를 줬습니다. 즉 최대,최소주변형률을 준 셈이 됩니다.
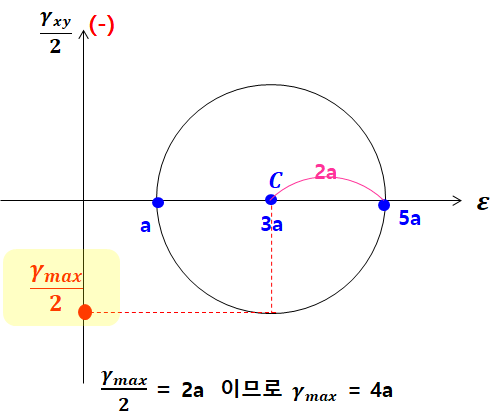
계속 언급했듯이 최대,최소주변형률은 모어원 좌표계에서 모어원 양 끝을 이루는 x축(평면변형률 축) 위의 점입니다. 즉 아래와 같이 그려지게 됩니다.
그럼 최대 전단변형률은 빨간색으로 표현된 바와 같이 [원의 반지름 x 2] 값, 4a가 됩니다.
#모어원,#모어원그리기,#모어원그리는법,#모어원문제,#변형률모어원,#모어원변형률문제,#주변형률,#전단변형률,#모어원전단변형률,#모어원개념,모어원설명,모어원작도,모어원공식,모어원이란,모어원부호
'STUDY > 기계공학 -재료역학' 카테고리의 다른 글
| 7. 보의 종류와 최대굽힘모멘트 (5) | 2020.03.03 |
|---|---|
| 6-5. 모어원 문제풀이 (4) | 2019.11.15 |
| 6-3. 모어원 그리는 방법 - 경사각 있을 때 (20) | 2019.10.27 |
| 6-2. 모어원 그리는 방법 - 경사각 없을 때 (1) (2) | 2019.10.26 |
| 6-1. 모어원 그리는 방법 - 배경지식편 (7) | 2019.10.26 |